全国统一QQ为:81308868、2027674726
全国统一邮箱为:youclunwen@163.com
全国统一咨询电话为:0757-63959708 ;15899573055
注册地址为:注册地址为:广东省佛山市禅城区同济西路12号永丰大厦A座1211号
全国统一邮箱为:youclunwen@163.com
全国统一咨询电话为:0757-63959708 ;15899573055
注册地址为:注册地址为:广东省佛山市禅城区同济西路12号永丰大厦A座1211号
1.本站所有合作期刊均为国家正规期刊,中华人民共和国新闻出版总署网(www.gapp.gov.cn)可查。
2.本网站承诺确保稿件质量,真诚为您服务,杜绝质量差的文章,为客户创造更高的价值。与您携手,创造更美好的明天。
2.本网站承诺确保稿件质量,真诚为您服务,杜绝质量差的文章,为客户创造更高的价值。与您携手,创造更美好的明天。
一类分数阶微分方程边值问题解的存在性与唯一性_压缩映射原理
发布日期:2022-10-15 11:15:00|
论文摘要:利用Banach压缩映射原理讨论非线性分数阶微分方程边值问题 论文关键词:压缩映射原理,格林函数,边值问题,微分 0引言: 分数阶微分方程在不同的科学领域起着越来越重要的作用。例如在扩散和运输理论、高分子材料的解链、弹性梁等诸多领域得以应用。近年来,有许多学者在分数阶微分方程领域取得了不少的成果. 本文受到文献[5]的启发,利用Banach压缩映射原理讨论下面含参数分数阶微分方程边值问题 解的存在性及唯一性,其中 1预备知识 为了方便证明,直接给出分数阶微分方程的定义和基本定理。 定义1.1:函数y: 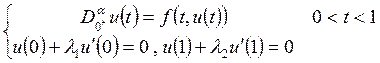 0 0定义1.2:函数y: 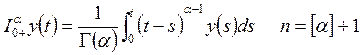 引理1.1:令 其中 引理1.2:令 其中 由引理1.1,引理1.2可得下面的引理。 引理1.3:给定 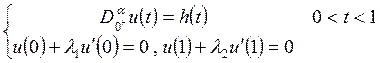 的唯一解是 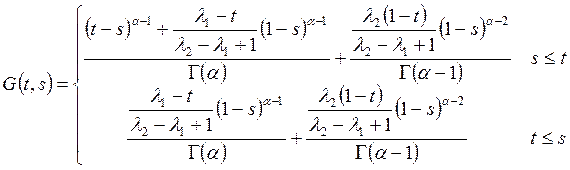 (2) (2)引理1.4:通过(2)定义的格林函数 (R1) (R2) 令 在本文中做以下假设: (H1)存在常数 考虑 定义算子T: 定理1.1(Banach压缩映射原理)设D是Banach空间X中的一个非空闭子集,而T: 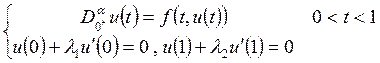 0,且T在D内满足Lipschitz条件,即对任意的 0,且T在D内满足Lipschitz条件,即对任意的2主要结果 定理2.1如果假设H1成立,且 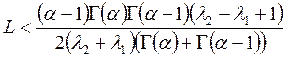 , ,那么边值问题(1)存在唯一解。 证明:令 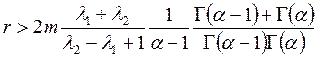 定义空间 由(H1),对 则 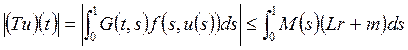 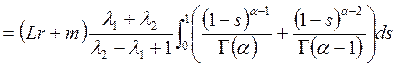 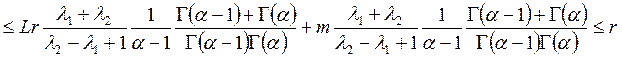 所以T: 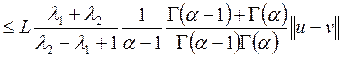 因为 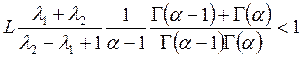 ,所以T是压缩映射,于是存在唯一的 ,所以T是压缩映射,于是存在唯一的 |
以上内容由论文代写网-优创网整理发布,详情请浏览http://www.youclunwen.com






